線形回帰(linear regression)
線形回帰について勉強したことを以下に纏めます。独学で勉強しただけなので、書いてあることが誤っていることがあるかもしれません。
なので書いてあることが絶対正しいと思わないで下さい。
点数を予測したい
あなたは塾の先生だとします。ある生徒から「テストで80点くらいを取りたいのだけど、一日何分くらい勉強すればいいの?」と聞かれました。
これを答えるために、他の生徒に勉強時間とテストの点数を聞きました。
| 人 | 時間(分) | 点数 |
|---|---|---|
| Aさん | 30 | 40 |
| Bさん | 40 | 50 |
| Cさん | 60 | 55 |
| Dさん | 90 | 65 |
| Eさん | 180 | 90 |
これをグラフに表すと以下のようになり
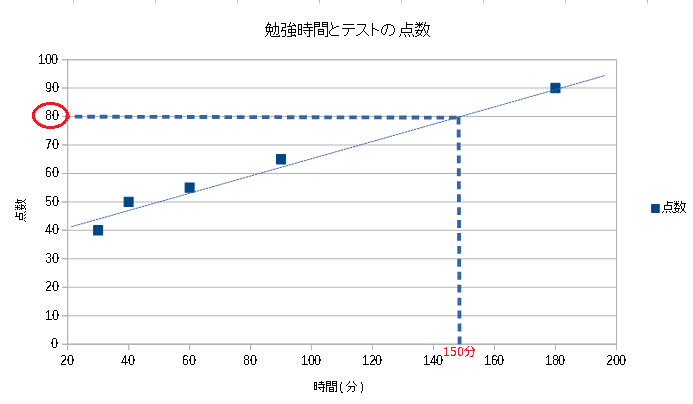
なんとなく「150分くらいじゃない」と答えられます。
AIに点数を予測させたい
上のグラフは、人間が適当に線を引きましたが、これをAIにやらせようとした場合を考えます。 今回は直線なので y = ax + bの1次関数になり、このaとbが求まれば、上のグラフのような線が引けます。
このように既存のデータに対し、y = ax + b のような計算式を当てはめ、a、bを求めることで未知の x に対し y
が予測できるようにすることを 線形回帰といいます。
※直線だから線形回帰ということではありません。定数×変数を繋げたようなものが分類されるため、下に出てくる重回帰、多項式回帰も線形回帰になります。
重回帰
今回は単純な y = ax + b のような1次関数の例に出しましたが、実際に使うときはaxに当たる部分が多く存在すると思います。(テストの点の例では、勉強時間:\(X_1\)、睡眠時間:\(X_2\)、基礎能力:\(X_3\)など)
\(Y=\beta_0+\beta_1X_1+\beta_2X_2+\beta_3X_3+ ・・・\)
このようにaxに当たる部分が複数存在するものを重回帰といい、これも線形回帰です。
(y = ax + b のようにxに当たるものが1つしか存在しないものを単回帰といいます)
多項式回帰
またデータの分布によって、1次関数では近似しきれない場合もあると思いますが、その場合は、2次関数~多項式を使用できます。 これを 多項式回帰 といい、これも線形回帰です。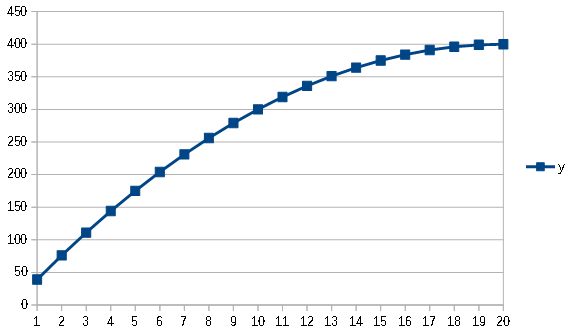
\(Y=\beta_0+\beta_1x+\beta_2x^2+\beta_3x^3+ ・・・\)
ページのトップへ戻る