ロジスティック回帰(Logistic regression)

今回はロジスティック回帰をやります。

独学で勉強しただけなので、書いてあることが誤っていることがあるかもしれません。
なので書いてあることが絶対正しいと思わないで下さい。

Yes/No を知りたい

線形回帰のときは点数を予測しましたが、今回は合格/不合格(Yes/No)のように答えが決まっているなかで、そのどれになるかをやります。

あなたは塾の先生だとします。
ある生徒から「〇〇を受験したいのだけど、一日何分くらい勉強すればいいの？」と聞かれました。
これを答えるために、先輩方に勉強時間と受験の結果を聞きました。

人	時間(分)	合格/不合格
Aさん	30	不合格
Bさん	40	不合格
Cさん	60	合格
Dさん	90	不合格
Eさん	180	合格

これをグラフに表そうとしても、グラフに表せず、答えることもできません。

シグモイド関数

線形回帰のように y = ax + b をそのまま使えないので少し変えます。

y = g(ax + b)

このようにg関数で囲むことによってyを0～1に変換します。
yが0ならNo、1ならYesのような使い方をします。

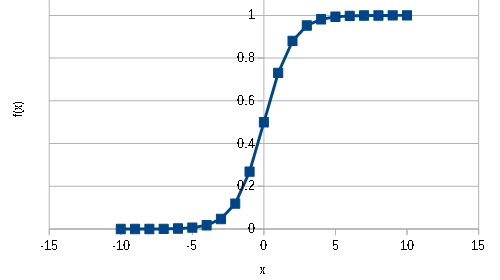
このg関数をシグモイド関数といいます。

\( f(x)=\dfrac{1}{1+e^{-x}}\ \)

シグモイド関数をグラフにすると以下のようになります。

y = ax + bとシグモイド関数を合わせると以下のようになります。
\( f(x)=\dfrac{1}{1+e^{-(ax + b)}}\ \)

この ax + b の部分が大きければ大きいほど1に近づき、小さければ小さいほど0に近づきます。
ax + b が0のときに、\(f(x)\)は0.5となり、YesともNoとも言える状態になります。

過去データよりa、bを求めることで、未知なるxがYes/Noのどちらか予測できるようになります。
このように二項分類ができるようにすることをロジスティック回帰(Logistic regression)といいます。

ページのトップへ戻る