TensorFlow 1次関数の係数を求める
今回はTensorFlowを使って1次関数の係数を求めてみます。サンプル
1次関数 y = W * x + b のWとbを求めてみます
import numpy as np
import tensorflow as tf
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'
# 1次関数 y = W * x + b のWとbを求めるサンプル
# yとxにサンプル値を入れて計算させてWとbを予想させる
# 1次関数の係数(W、b)となる変数を定義。初期値は両方5.0
W = tf.Variable([5.0], dtype=tf.float32)
b = tf.Variable([5.0], dtype=tf.float32)
# 1次関数のx,yの入れ物を定義
x = tf.placeholder(tf.float32)
y = tf.placeholder(tf.float32)
# 1次関数を定義
keisan = W * x + b
# サンプルの計算値とyの差を2乗(tf.square)したものを
# すべて足し合わせる処理(tf.reduce_sum)の定義
loss = tf.reduce_sum(tf.square(keisan - y))
# ↑で定義した差の2乗の合計値がより小さくなるように操作する処理を定義
# 2乗させないと差はマイナス値になり、どこまでも小さくなる。
# 2乗させることでマイナス値はなくなる(-1 * -1 = 1)
optimizer = tf.train.GradientDescentOptimizer(0.01)
train = optimizer.minimize(loss)
# x,yにセットされるサンプルデータ
# y = 2 * x + 1 となるようなデータを用意
x_sample = [1, 2, 3, 4, 5]
y_sample = [3, 5, 7, 9, 11]
# 定義してきたもの処理を開始する
sess = tf.Session()
# 変数を使用するため以下で初期化
sess.run(tf.global_variables_initializer())
# 処理のメイン
for i in range(1000):
# Wとbの変数の変わり具合を表示
print("W(2が正解):" + str(sess.run(W)) + "\tb(1が正解):" + str(sess.run(b)))
# 変数の調整
sess.run(train, {x: x_sample, y: y_sample})
イメージ
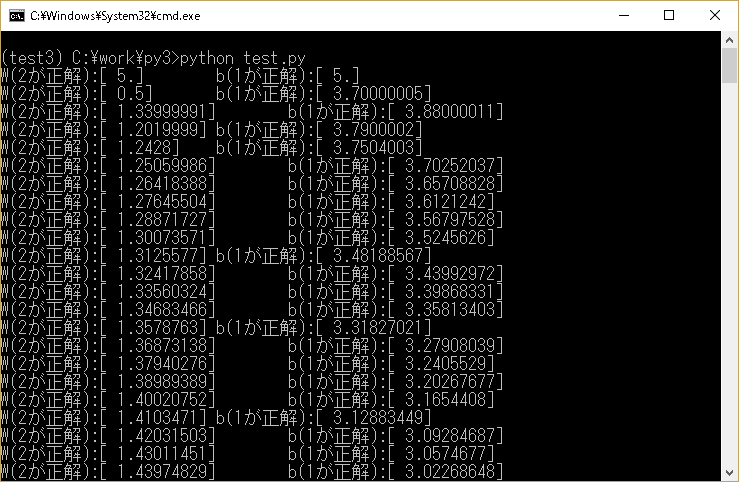
W、bに初期値として5をセットして処理を開始したので、最初に5で計算して、だんだんW→2、b→1に近くなります。
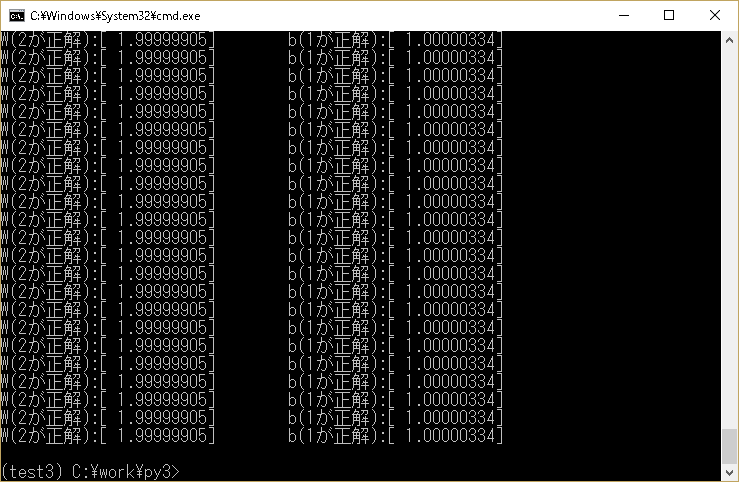
最終的にはW→1.99999905、b→1.00000334で落ち着きました。
もっと単純なサンプル
Wが5からスタートして100になるまでの変化を見てみます
import tensorflow as tf
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'
# W = 100 を求めるサンプル
# 変数を定義。初期値は5.0
W = tf.Variable([5.0], dtype=tf.float32)
# 変数Wと100の差を2乗(tf.square)したものを定義
loss = tf.square(W - 100)
# ↑で定義した差の2乗の合計値がより小さくなるように操作する処理を定義
# 2乗させないと差はマイナス値になり、どこまでも小さくなる。
# 2乗させることでマイナス値はなくなる(-1 * -1 = 1)
optimizer = tf.train.GradientDescentOptimizer(0.3)
train = optimizer.minimize(loss)
# 定義してきたもの処理を開始する
sess = tf.Session()
# 変数を使用するため以下で初期化
sess.run(tf.global_variables_initializer())
# 処理のメイン
for i in range(21):
# Wとbの変数の変わり具合を表示
print("W(100が正解):" + str(sess.run(W)))
# 変数の調整
sess.run(train)
イメージ
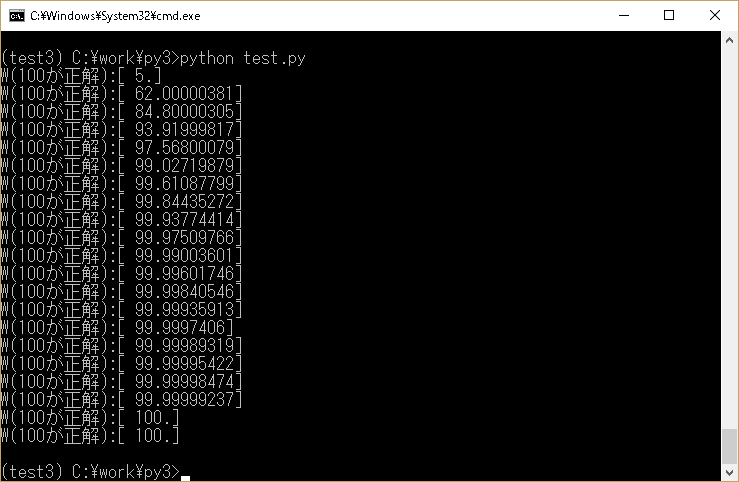
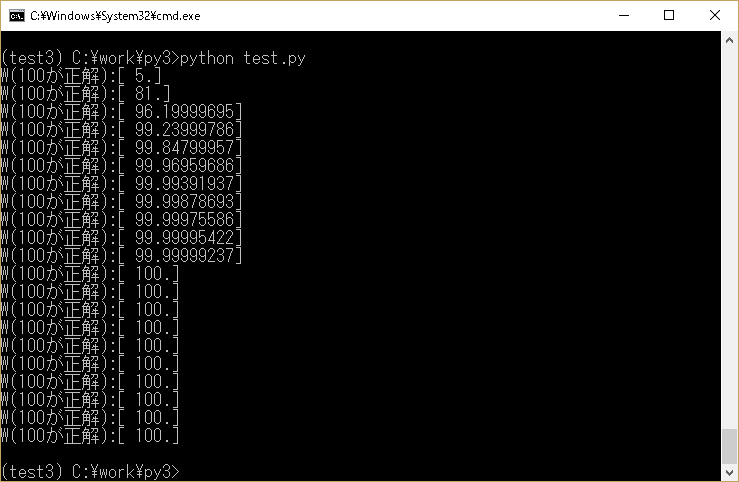
tf.train.GradientDescentOptimizerに渡す値を0.3→0.4にすると、もっと早く100に辿り着きます
イメージ
ページのトップへ戻る